
Попробуй новый сервис "Траектория"! Искусственный интеллект построит карьерную траекторию для освоения профессии твоей мечты и найдет нужные курсы.
язык курса
длительность курса
понадобится для освоения
для зачета в своем вузе
Пользователи курса смогут овладеть вторым разделом курса Теоретическая механика. В курсе наглядно, в сочетании с математической строгостью, рассматривается движение материальной точки и твердого тела и механической системы на основе базовых понятий и теорем механики. Традиционный теоретический материал сопровождается разбором практико-ориентированных задач с составлением 2D- и 3D расчетных схем. Курс выгодно отличается от традиционных курсов по Теоретической механике наличием анимации, которая позволяет наглядно понять общие законы взаимодействия и движения материальных объектов.
Данный курс ориентирован на реализацию образовательных программ по направлениям подготовки из области образования «Инженерное дело, технологии и технические науки». Курс содержит систематизированное изложение основных понятий и принципов механики, описание методов математического моделирования инженерных конструкций и типовых машин и механизмов. Содержание курса ориентировано на подготовку к восприятию последующих дисциплин, формирующих направленность образовательной программы.
Курс рассчитан на 16 недель. Недельная нагрузка обучающегося по курсу - 8 академических часов.
Еженедельные занятия будут включать:
· просмотр тематических видео-лекций с анимацией;
· просмотр тематических видео-семинаров с решением типовых задач;
· самостоятельное изучение примеров;
· выполнение многовариантных теоретических тестовых заданий с автоматизированной проверкой результатов;
· выполнение многовариантных заданий по решению практических задач с автоматизированной проверкой результатов
Предусмотрено промежуточное контрольное тестирование по каждому разделу курса.
1. Курс теоретической механики / Под ред. К.С.Колесникова. – М.: Изд. МГТУ им. Н.Э. Баумана, 2005, 2007, 2011, 2017 - 736 с.
2. Никитин Н.Н. Курс теоретической механики. – М.: Высшая школа, 2003, 2005 и более поздние издания. – 719 с.
3. Сборник задач по теоретической механике / Под ред. К.С.Колесникова – М.: Наука, 2007, 2008 и более поздние издания. – 448 с.
4. Мещерский И.В. Задачи по теоретической механике: Учебное пособие. – СПб.: Лань, 2010 – 448 с.
5. Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической механики.– СПб.: Лань, 2009.
6. Тарг С.М. Краткий курс теоретической механики. Учебник. – М.: Высшая школа, 2008. - 415 с.
7. Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах. – М.: Наука, тт. 1-3, 1966 г. и след.
8. Саратов Ю.С., Баранов В.Н., Нарская Н.Л. Динамика материальной точки. Методические указания к курсовой работе по теоретической механике. – М.: Изд-во МГТУ им. Н.Э. Баумана, 1999.
9. Общие теоремы динамики. Метод. указания по выполнению курсовой работы. / В.В. Дубинин, Н.Н. Никитин, О.П. Феоктистова. – М.: Изд-во МГТУ им. Н.Э. Баумана, 1989.
10. Витушкин В.В., Максимов Г.М., Русанов П.Г. Избранные принципы аналитической механики. Уравнения Лагранжа 2-го рода: Метод. указания к выполнению курсовой работы по теоретической механике. М.: Изд-во МГТУ им. Н.Э. Баумана, 2004.
11. Витушкин В.В., Максимов Г.М. Избранные принципы аналитической механики. Уравнения Лагранжа 2-го рода: Метод. указания к выполнению курсовой работы по теоретической механике. / Под ред. В.В. Дубинина. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2012.
12. Лямин В.И., Темнов А.Н. Аналитическая механика. М.: Изд-во МГТУ им. Н.Э. Баумана, 1990.
Изучение курса предполагает предварительное освоение следующих дисциплин:
|
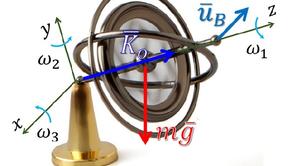
Неделя 1. Динамика материальной точки. Основные положения динамики. Аксиомы динамики Ньютона. Инерциальная система отсчета. Дифференциальные уравнения динамики точки в векторной форме и в проекциях на декартовы и естественные оси координат. Две основные задачи динамики точки. Интегралы уравнений движения точки. Случай несвободного движения материальной точки. Неделя 1. Решение задач Неделя 2. Дифференциальные уравнения движения точки в неинерциальной системе отсчета, динамическая теорема Кориолиса. Принцип относительности Галилея-Ньютона. Равновесие и движение точки относительно поверхности Земли. Неделя 2. Решение задач Тестирование по результатам недель 1-2 Неделя 3. Механическая система. Классификация сил, действующих на механическую систему: силы внешние и внутренние. Равенство нулю главного вектора и главного момента внутренних сил. Масса системы. Центр масс системы и его координаты. Дифференциальные уравнения движения механической системы. Теорема о движении центра масс системы. Закон сохранения движения центра масс. Дифференциальные уравнения поступательного движения твердого тела. Количество движения материальной точки и механической системы. Элементарный импульс и импульс силы за конечный промежуток времени, проекции на координатные оси. Теорема об изменении количества движения в дифференциальной и конечной формах. Закон сохранения количества движения системы. Неделя 3. Решение задач Неделя 4. Моменты инерции системы и твердого тела относительно оси и полюса. Радиус инерции. Теорема Штейнера, вычисление моментов инерции тел простейшей формы. Момент количества движения точки относительно центра и оси. Главный момент количеств движения (кинетический момент) механической системы относительно центра и оси. Кинетический момент твердого тела относительно оси вращения. Теорема об изменении кинетического момента системы. Закон сохранения кинетического момента. Дифференциальное уравнение вращения твердого тела вокруг неподвижной оси. Движение точки под действием центральной силы. Понятие о секторной скорости. Теорема площадей. Неделя 4. Решение задач Неделя 5. Кёнигова система отсчета. Формула для кинетического момента системы материальных точек при сложном движении. Теорема об изменении кинетического момента системы материальных точек в относительном движении по отношению к центру масс. Дифференциальные уравнения плоского движения твердого тела. Неделя 5. Решение задач Неделя 6. Элементарная и полная работа силы. Мощность. Работа равнодействующей силы. Работа внутренних сил системы, работа сил, приложенных к твердому телу, при его различных движениях. Неделя 6. Решение задач Неделя 7. Кинетическая энергия точки и системы точек. Вычисление кинетической энергии при сложном движении (теорема Кенига). Кинетическая энергия твердого тела в различных случаях его движений. Теорема об изменении кинетической энергии для точки и системы материальных точек. Неделя 7. Решение задач Неделя 8. Потенциальное силовое поле. Элементарная и полная работа силы в потенциальном силовом поле. Силовая функция и потенциальная энергия поля. Условия существования силовой функции. Поверхности уровня и их свойства. Примеры вычисления силовых функций: однородного поля силы тяжести, линейной силы упругости, поля притяжения по закону Ньютона. Закон сохранения полной механической энергии системы. Тестирование по результатам недель 3-8 Неделя 9. Принцип Даламбера для материальной точки, сила инерции. Принцип Даламбера для механической системы. Главный вектор и главный момент сил инерции. Приведение сил инерции твердого тела к центру в общем и частных случаях движения твердого тела. Определение с помощью принципа Даламбера динамических реакций при несвободном движении точки и механической системы - метод кинетостатики. Неделя 9. Решение задач Неделя 10. Связи и их классификация. Возможные перемещения точки и механической системы. Обобщенные координаты. Вариации обобщенных координат. Число степеней свободы голономной системы. Элементарная работа силы на возможном перемещении. Идеальные связи. Принцип возможных перемещений (принцип Лагранжа). Неделя 10. Решение задач Неделя 11. Общее уравнение динамики (принцип Даламбера-Лагранжа). Пример. Обобщенные силы. Различные способы вычисления обобщенных сил. Обобщенные силы в случае потенциального силового поля. Условия равновесия в обобщенных силах. Равновесие системы в потенциальном поле. Общее уравнение динамики в обобщенных силах. Неделя 11. Решение задач Неделя 12. Уравнения Лагранжа 2 рода. Вывод и методика применения. Неделя 12. Решение задач Неделя 13. Геометрия масс. Момент инерции тела относительно оси, проходящей через заданную точку в заданном направлении. Формула для вычисления момента инерции относительно оси любого направления. Центробежные моменты инерции. Тензор инерции. Эллипсоид инерции. Главные центральные оси инерции и их свойства. Неделя 13. Решение задач Тестирование по результатам недель 9-13 Неделя 14. Движение твердого тела вокруг неподвижной точки. Кинетический момент твердого тела относительно неподвижной точки, его проекции на оси координат. Кинетическая энергия твердого тела с одной неподвижной точкой. Вывод динамических уравнений Эйлера. Обзор случаев интегрируемости уравнений движения с одной закрепленной точкой (случаи Эйлера, Лагранжа, Ковалевской). Неделя 15. Элементы приближенной теории гироскопа. Основные понятия и допущения. Теорема Резаля. Особенности движения оси гироскопа. Закон прецессии. Гироскопический момент. Определение гироскопических реакций, правило Жуковского. Примеры применения гироскопов в технике. Неделя 15. Решение задач Неделя 16. Итоговое тестирование |
|
В результате освоения курса «Теоретическая механика. Динамика» студент будет знать:
В результате освоения курса «Теоретическая механика. Динамика» студент будет уметь:
В результате освоения курса «Теоретическая механика. Динамика» студент будет владеть:
язык курса
длительность курса
понадобится для освоения
для зачета в своем вузе

Кандидат физико-математических наук, Доцент
Должность: Доцент кафедры «Теоретическая механика» МГТУ им. Н.Э.Баумана

Кандидат физико-математических наук, Доцент
Должность: Доцент кафедры «Теоретическая механика» МГТУ им. Н.Э.Баумана

Кандидат технических наук, Доцент
Должность: Доцент кафедры «Теоретическая механика» МГТУ им. Н.Э.Баумана